卷积神经网络基础：常用层和经典网络的介绍

学习
3249 字
17 分钟

1. 卷积神经网络的基本操作#

1.1. 卷积层#

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算，其运算的形象解释如图：

卷积操作

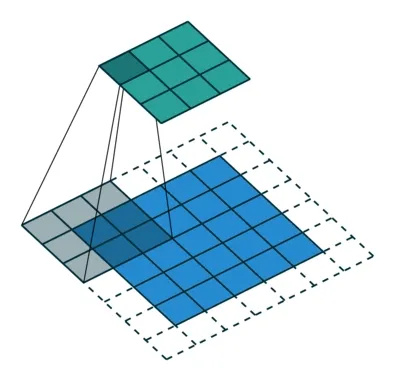
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0)

:::note 常用参数

参数默认值说明
in_channels必需输入通道数
out_channels必需输出通道数
kernel_size必需卷积核大小
stride1相关运算的步长，可以是单个数字或一个元组
padding0应用于输入的填充，表示在两侧应用的隐式填充量

:::

1.2. 池化层#

最大值池化：对在池化核内的数字取最大值。

torch.nn.MaxPool2d(kernel_size, stride=None, padding=0)

平均值池化：对在池化核内的数字取平均。

torch.nn.AvgPool2d(kernel_size, stride=None, padding=0)

:::note 常用参数

参数默认值说明
kernel_size必需池化核大小
strideNone池化操作的步长，可以是单个数字或一个元组，默认为None，大小和kernel_size相同
padding0应用于输入的填充，表示在两侧应用的填充量

:::

1.3. 转置卷积#

转置卷积操作能够让矩阵的大小增大，常用于语义分割。 转置卷积

torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0)

转置卷积的参数和卷积运算相对应，相同参数的卷积和转置卷积可视为对矩阵形状的逆预算。

1.4. 正则化#

L1正则: Ω(w)=∑i∥wi∥2\Omega(w) = \sum_i \Vert w_i \Vert_2 对各项平均值求和
L2正则: Ω(w)=∑i∥wi∥1\Omega(w) = \sum_i \Vert w_i \Vert_1 对各项平方求和

L2正则倾向让参数更分散 (spread out) 。 :::note 例 如果有两组参数： w1=[1,0,0,0]w_1 = [1, 0, 0, 0] 和 w2=[0.25,0.25,0.25,0.25]w_2 = [0.25, 0.25, 0.25, 0.25]， 对于L1正则来说，两者对应正则项相等；而L2正则则不同。
简言之，L2正则倾向于让参数更“分散”。 :::

1.5. 优化器#

随机梯度下降 (SGD)#

在pytorch中的SGD优化器默认使用一个batchsize的样本进行计算，实质上为小批量梯度下降 (Mini-Batch Gradient Descent)

optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3, momentum=0.9) # 加入动量

:::note 常用参数

参数默认值说明
params必需要优化的模型参数。通常传入 model.parameters()。
lr必需学习率，控制参数更新的步长。
momentum0动量因子。引入“惯性”，帮助加速收敛并减少震荡。常用值：0.9。
weight_decay0权重衰减（L2 正则化）。用于防止过拟合，对所有参数施加 L2 惩罚。常用值：1e-4。
dampening0动量的阻尼系数。在 nesterov=True 时有用，一般保持为 0。
nesterovFalse是否使用 Nesterov 动量。能提供更优的收敛性能，常与 momentum 搭配使用。

:::

TIP

Momentum 动量梯度下降
Momentum 主要引入了基于梯度的移动指数加权平均的思想，即当前的参数更新方向不仅与当前的梯度有关，也受历史的加权平均梯度影响。

Adam#

Adam (Adaptive Moment Estimation) 结合了动量法 (Momentum) 和 RMSProp 的思想， 旨在通过计算梯度的一阶矩估计和二阶矩估计来调整每个参数的学习率，从而实现更高效的网络训练。

optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

:::note 常用参数

参数默认值说明
params必需要优化的模型参数，通常为 model.parameters()。
lr1e-3学习率。Adam 的默认值 1e-3 通常适合大多数任务。
betas(0.9, 0.999)用于计算梯度及其平方的指数移动平均的系数，相当于动量参数。
eps1e-8数值稳定性的小常数，防止除零。一般无需修改。
weight_decay0权重衰减（L2 正则化），用于防止过拟合。常用值：1e-4。
amsgradFalse是否使用 AMSGrad 变体，可改善收敛性（尤其在某些 NLP 任务中）。

:::

AdamW#

AdamW 是 Adam 优化器的重要改进版本，它正确地解耦了权重衰减和梯度归一化。 将权重衰减作为独立的更新项，不参与梯度计算；权重衰减不受自适应学习率缩放，真正实现了“解耦”。

optimizer = torch.optim.AdamW(model.parameters(), lr=1e-3, weight_decay=1e-2)

:::note 常用参数 torch.optim.AdamW 的参数与 Adam 非常相似，主要不同为weight_decay。

参数默认值说明
params必需要优化的模型参数，通常为 model.parameters()。
lr1e-3学习率。AdamW 通常也使用 1e-3 或 5e-4。
betas(0.9, 0.999)一阶和二阶矩估计的指数衰减率，同 Adam。
eps1e-8数值稳定性的小常数，防止除零。一般无需修改。
weight_decay1e-2解耦的权重衰减（L2 正则化），这是 AdamW 的核心改进。
amsgradFalse是否使用 AMSGrad 变体，可改善收敛性（尤其在某些 NLP 任务中）。

:::

1.6. 暂退法(Dropout)#

每个中间活性值 hh 以暂退概率 pp 由随机变量 h′h' 替换，根据此模型的设计，其期望值保持不变，即 E[h′]=hE[h'] = h。

h′={0概率为ph1−p其他h' = \begin{cases} 0 &\text{概率为p}\\ \frac{h}{1-p} &\text{其他} \end{cases}

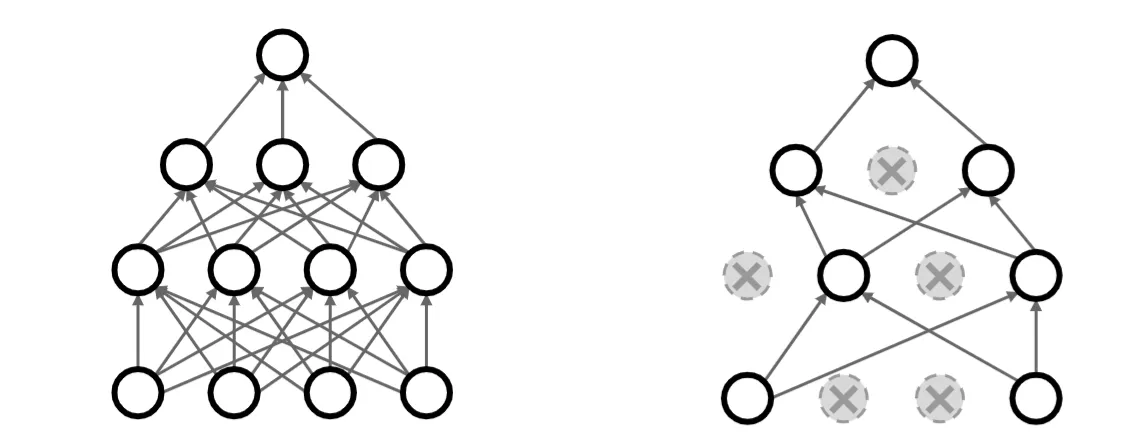
dropout

Dropout 的 pytorch 实现

torch.nn.Dropout(p=0.5, inplace=False)

:::note 常用参数

参数默认值说明
p0.5在训练过程中，以概率 p 随机将输入张量的一些元素置为零
inplaceFalse如果设置为 True ，将就地执行此操作(不推荐)

:::

1.7. 批量归一化 (batch normalization)#

批量归一化，又叫纵向归一化。基于当前小批量 (batch size) 的数据，归一化输入，即通过减去其均值并除以其标准差。

TIP

引入批量归一化能够改善是收敛性，同时减少了对其他形式的规范化的需求。
其原因在于对网络每层归一化后，神经网络输入的分布更稳定，从而提升网络的训练效率。 从另一方面来说，我们可以认为批量归一化避免神经网络去学习每层数据分布的过程，因此收敛速度更快。

批量归一化可看作神经网络中的一层：

torch.nn.BatchNorm()

1.8. 层归一化 (Layer Normalization)#

层归一化，又叫横向归一化。对上一个隐藏层 (hidden layer) 的输出进行归一化，使该层的数据分布稳定。

LayerNorm中不会像BatchNorm那样跟踪统计全局的均值方差，因此train()和eval()对LayerNorm没有影响，即在eval模式下，只有BatchNorm会屏蔽，其他Norm函数不会屏蔽。

层归一化在 pytorch 中的实现：

torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, bias=True, device=None, dtype=None)

:::note 常用参数

参数默认值说明
normalized_shape必需该层的特征维度，即要被标准化的维度
eps1e-05分母修正项
elementwise_affineTrue是否需要affine transform，这里也提醒你是逐元素的仿射变换
biasTrue如果设置为 False ，则层将不会学习加性偏差（仅在 elementwise_affine 为 True 时有效）

:::

2. 经典卷积神经网络#

2.1. 深度卷积神经网络(AlexNet)#

AlexNet和LeNet的架构非常相似，如下图所示。在这里提供的是一个稍微精简版本的AlexNet： LeNet和AlexNet

AlexNet的pytorch代码实现

net = nn.Sequential(
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 1000)
)

2.2. 使用块的网络(VGG)#

与AlexNet、LeNet一样，VGG网络可以分为两部分：第一部分主要由卷积层和汇聚层组成，第二部分由全连接层组成。 从AlexNet到VGG，它们本质上都是块设计。 VGG

我们使用 vgg_block 函数定义了一个VGG块。

def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2, stride=2))
    return nn.Sequential(*layers)

使用该 vgg_block 函数能够方便的定义出不同的VGG网络。

2.3. 网络中的网络(NiN)#

最初的NiN网络是在AlexNet后不久提出的，NiN和AlexNet之间的一个显著区别是NiN完全取消了全连接层。 相反，NiN使用一个NiN块，其输出通道数等于标签类别的数量。 NiN

我们使用 nin_block 函数定义了一个NiN块

def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

NiN设计的一个优点是，它显著减少了模型所需参数的数量。然而，在实践中，这种设计有时会增加训练模型的时间。

2.4. 含并行连接的网络(GooLeNet)#

在GoogLeNet中，基本的卷积块被称为Inception块(Inception block)。

Inception块的结构

Inception块的代码实现如下：

class Inception(nn.Block):
    # c1--c4是每条路径的输出通道数
    def __init__(self, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2D(c1, kernel_size=1, activation='relu')
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2D(c2[0], kernel_size=1, activation='relu')
        self.p2_2 = nn.Conv2D(c2[1], kernel_size=3, padding=1, activation='relu')
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2D(c3[0], kernel_size=1, activation='relu')
        self.p3_2 = nn.Conv2D(c3[1], kernel_size=5, padding=2, activation='relu')
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2D(pool_size=3, strides=1, padding=1)
        self.p4_2 = nn.Conv2D(c4, kernel_size=1, activation='relu')


    def forward(self, x):
        p1 = self.p1_1(x)
        p2 = self.p2_2(self.p2_1(x))
        p3 = self.p3_2(self.p3_1(x))
        p4 = self.p4_2(self.p4_1(x))
        # 在通道维度上连结输出
        return np.concatenate((p1, p2, p3, p4), axis=1)

GoogLeNet一共使用9个Inception块和全局平均汇聚层的堆叠来生成其估计值，Inception块之间的最大汇聚层可降低维度。

GooLeNet结构

2.5. 残差网络(ResNet)#

随着网络的设计不断加深，如何使新添加的层变的至关重要。
对于非嵌套的函数类较复杂的函数类并不能保证更接近真函数， 因此，只有当较复杂的函数类包含较小的函数类时，我们才能确保提高它们的性能。 嵌套函数类和非嵌套函数类对比

假设我们的原始输入为 xx ，而希望学出的理想映射为 f(x)f(x) 。左图虚线框中的部分需要直接拟合出该映射 f(x)f(x) ， 而右图虚线框中的部分则需要拟合出残差映射 f(x)−xf(x) - x 。残差映射在现实中往往更容易优化。 残差块结构

特别地，当输入和输出通道数不同时，我们要通过一个1×11 \times 1的卷积层调整通道和分辨率。 带有卷积层的残差块

残差块pytorch的实现如下：

class Residual(nn.Block):
    def __init__(self, num_channels, use_1x1conv=False, strides=1, **kwargs):
        super().__init__(**kwargs)
        self.conv1 = nn.Conv2D(num_channels, kernel_size=3, padding=1, strides=strides)
        self.conv2 = nn.Conv2D(num_channels, kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2D(num_channels, kernel_size=1, strides=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm()
        self.bn2 = nn.BatchNorm()


    def forward(self, X):
        Y = npx.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        return npx.relu(Y + X)

2.6. 稠密连接网络(DenseNet)#

稠密连接网络(DenseNet)在某种程度上是ResNet的逻辑扩展。ResNet 与 DenseNet 在跨层连接上的主要区别：使用相加和使用连结。 DenseNet和ResNet的对比

DenseNet输出是连接 [,][,] ，在应用复杂的函数序列后，得到 xx 到其展开式的映射：

x→[x,f1(x),f2([x,f1(x)]),f3([x,f1(x),f2([x,f1(x)])]),...]x \rightarrow [x, f_1(x), f_2([x, f_1(x)]), f_3([x, f_1(x), f_2([x, f_1(x)])]), ...]

稠密连接

稠密网络主要由2部分构成：稠密块(dense block)和过渡层(transition layer)。 前者定义如何连接输入和输出，而后者则控制通道数量，使其不会太复杂。

一个稠密块由多个卷积块组成，每个卷积块使用相同数量的输出通道。然而，在前向传播中，我们将每个卷积块的输入和输出在通道维上连结。

def conv_block(num_channels):
    blk = nn.Sequential()
    blk.add(nn.BatchNorm(),
            nn.Activation('relu'),
            nn.Conv2D(num_channels, kernel_size=3, padding=1))
    return blk


class DenseBlock(nn.Block):
    def __init__(self, num_convs, num_channels, **kwargs):
        super().__init__(**kwargs)
        self.net = nn.Sequential()
        for _ in range(num_convs):
            self.net.add(conv_block(num_channels))


    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            # 连接通道维度上每个块的输入和输出
            X = np.concatenate((X, Y), axis=1)
        return X

由于每个稠密块都会带来通道数的增加，使用过多则会过于复杂化模型。而过渡层可以用来控制模型复杂度。 它通过1×11 \times 1卷积层来减小通道数，并使用步幅为2的平均汇聚层减半高和宽，从而进一步降低模型复杂度。

def transition_block(num_channels):
    blk = nn.Sequential()
    blk.add(nn.BatchNorm(), nn.Activation('relu'),
            nn.Conv2D(num_channels, kernel_size=1),
            nn.AvgPool2D(pool_size=2, strides=2))
    return blk

参考资料#

  1. 动手学深度学习
  2. 李飞飞·斯坦福CS231n计算机视觉课程
卷积神经网络基础：常用层和经典网络的介绍
https://blog.rinne05.top/blog/learning/deep-learning/convnet-intro/
作者
霖
发布于
9/12/2025
许可协议
CC BY-NC-SA 4.0
Kaggle项目中训练模型时的技巧总结
基于深度学习的多目标跟踪

主题设置

主题模式
主题色
透明度
模糊
© 2025 霖，采用 CC BY-NC-SA 4.0 许可
ICP备案号: 豫ICP备2025156598号-1
输入以搜索...
通过 Fuse.js 搜索